Estimating the 3D layout of indoor scenes and its clutter from depth sensors. - Zhang et al.
Zhang, J., Kan, C., Schwing, A. G., & Urtasun, R. (2013). Estimating the 3D layout of indoor scenes and its clutter from depth sensors. Proceedings of the IEEE International Conference on Computer Vision, 1273–1280. https://doi.org/10.1109/ICCV.2013.161
Abstract
RGB-D data를 사용하여 indoor environment의 layout과 clutter를 jointly estimation한다.
layout은 실내 공간을 이루는 벽, 바닥 천장을 의미하고, clutter는 '잡동사니' 라는 의미로, 가구와 같이 layout을 제외한 물체들을 뜻한다.
즉 RGB-D 데이터를 가지고 실내 공간을 파악해본다는 것이다.
RGB(apperance)와 Depth는 서로 complementary한 정보를 담고 있기 때문에 이를 이용하여 estimation 성능을 높였다.
저자는 이를 "inherent decomposition of additive potential" 이라고 부르는데, 직역하면 "추가적인 잠재력(Depth 정보를 말하는듯?)에 대한 내재적 분해" 정도인데 몇번을 읽어봐도 무슨 소린지 모르겠다.
아무튼 이렇게 Depth를 사용하는 것이 NYU v2에서 테스트했을 때 layout estimation error는 6%, Clutter estimation error는 13% 감소시킨다는 것을 증명하였다.
Introduction
Sementic parsing approache는 RGB-D를 활용하여 방의 basic components를 추정하려고 시도한다. (벽, 바닥, 천장)
이 방법은 효과적이긴 하지만 문제의 구조적 성질 (실재 공간은 Manhattan World Assumption을 만족하고, 각 면들은 서로 orthonormal한 점)을 활용하지 못한다.
이러한 성질들은 monocular setting (단일 RGB 이미지로부터 layout을 추정하는 것)에서는 널리 사용되지만, RGB-D를 이용하여 layout을 추정할때는 이런 성질들이 고려되지 않았다.
추가적으로, 자동화를 위해서 layout뿐만 아니라 clutter를 추정하는 방법도 제안한다.
clutter는 벽, 바닥, 천장같이 방의 basic component를 제외한 가구같은 실내의 물체를 의미한다.
appearance와 depth 두 complementary feature를 사용하여 이를 두 task의 dependency를 사용하는 joint estimation problem으로 정의하여 문제를 풀었다.
제안하는 decomposition method는 구성한 additive energy(loss 개념인듯)을 최대 2개의 변수를 포함한 Markov Random Field로 decompose한다.
제안한 방법에 의해 clutter로 label된 super-pixel은 가구 class로 추정할 수 있다.
이를 통해 Fig.1과 같이 RGB-D 이미지를 이용해 room layout, clutter 추정 뿐만 아니라 semantic segmentation도 가능하다.
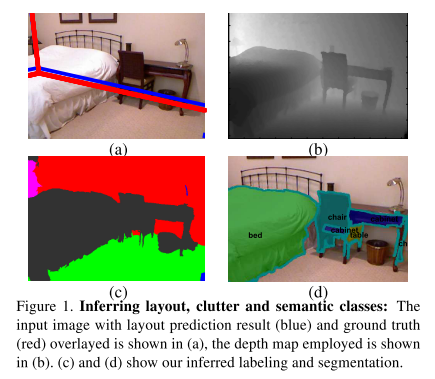
또한 NYU v2 dataset을 사용하여 효율성을 증명하였다. 6%의 layout, 13%의 clutter estimation에서 성능 향상이 있었다.
이는 clutter가 depth image에서 foreground에 해당하므로 쉽게 구별되기 때문으로 여겨진다.
Realated Work
생략
Joint Layout and Clutter Labeling
Apperance와 depth를 모두 활용한 전체적인 방법을 설명
첫번째로는 depth를 이용해서 거 나은 superpixel을 얻는다.
그 다음에 얻어진 superpixel과 layout을 표현하는 random 변수에 동작하는 joint model을 설계한다.
그 다음에 학습과 추론 과정에 대해 설명한다.
1) Superpixel Esimation
특정 물체의 일부분에 해당하는 평면을 표현하는 각 superpixel을 구별해낸다.
K. Yamaguchi 등에 따르면 R. Achanta 등이 제시한 SLIC을 확장시켜 apperance와 depth를 모두 활용하도록 수정하였다.
segmentation 문제를 세개의 energy의 합을 최소화 시키는 문제로 표현하였다.
그 세가지 energy란: encoding shape, apperance, depth 이다.
$E_{loc}$: location energy로 superpixel이 균일한 모양을 가지고 있다는 사실을 표현.
$E_{depth}$: superpixel의 depth는 부분적으로 평면에 가깝다는 사실을 표현.
$E_{app}$: superpixel로 합쳐진 pixel들이 모두 비슷한 apperance를 가지고 있다는 사실을 표현.
$s_p\in \left \{ 1,\cdots K \right \}$ : $s_p$는 pixel $\mathbf{p}$가 superpixel에 할당하는 임의 변수 일 때,
$$E\left (\mathbf{p},s_p,\mu _p,c_{s_{p}},D_{s_{p}} \right ) =E_{loc}\left ( \mathbf{p},s_p \right )+\lambda _a E_{app}\left ( \mathbf{p},s_p,c_{s_{p}} \right )+\lambda _d E_{depth}\left ( \mathbf{p},s_p,c_{s_{p},g_{s_{p}}} \right )$$
각 energy term을 다음과 같이 정의한다.
$$E_{loc}\left ( \mathbf{p},s_p \right )=\left \| \mathbf{p}-\mu_{s_{p}} \right \|^2_2, $$
$$E_{app}\left ( \mathbf{p},s_p,c_{s_{p}} \right )=\left \| I\left (\mathbf{p} \right ) -c_{s_{p}} \right \|^2_2,$$
$$E_{depth}\left ( \mathbf{p},s_p,c_{s_{p},g_{s_{p}}} \right )=\left \| \bigtriangledown d \left (\mathbf{p} \right ) -g_{s_{p}} \right \|^2_2, $$
이 때 $\mu_{s_{p}}$는 superpixel $s_p$의 mean position이다. 따라서 $E_{loc}$는 pixel $\mathbf{p}$가 superpixel의 평균으로부터 얼마나 떨어져 있느냐를 의미
$c_{s_{p}}$는 실험 환경의 mean descriptor인데, 전체 pixel에 대한 destriptor를 평균낸 값이라고 생각하면 될듯.
$g_{s_{p}}$는 mean depth gradient descriptor로, $ \bigtriangledown d \left (\mathbf{p} \right ) $는 depth gradient를 의미한다.
전체 energy term $E$를 최소하 하는 최적화 문제.
이 문제를 assignment $s$를 푸는 과정과 $g, \mu, c$를 푸는 과정을 번갈아가면서 진행한다.
2) Joint Model
위 과정을 거쳐 depth cue를 활용하여 이미지를 superpixel로 나누었다.
이제는 layout, labeling 변수를 고려하여 에너지를 정의한다.
joint model은 labeling, layout 작업에서 CRF로 정의된다.
각각의 superpixel은 $\left x_i \in { \left \{ clutter,left,right,front,ceiling,floor \right \}=L $중 하나로 labeling된다. (labeling task)
최근의 monocular approach들을 따라서, layout task는 두개의 다른 VP로부터 나오는 ray로 표현될 수 있다.
layout problem은 네개의 파라미터 $ \mathbf{y}=\right \{ y_1, y_2, y_3, y_4 \left \} $ 로 나타내어 질 수 있다.

System의 전체 engergy는 layout task, labeling task, 그리고 두 task간의 관계에 관한 compatibility term으로 구성된다.
$$ E \left ( \mathbr{x},\mathbr{y} \right ) = E_{layout} \left ( \mathbr{y} \right ) +E \left ( \mathbf{x},\mathbf{y} \right ) = E_{layout} \left ( \mathbf{y} \right ) +E_{labeling} \left ( \mathbf{x} \right ) + E_{comp} \left ( \mathbf{x}, \mathbf{y} \right ) $$
Layout Energy
monocular approach를 따라서 layout의 energy를 직육면체의 면 $\alpha$에 대한 에너지의 합으로 정의함
각 5면에 대해서 weighted sum으로 표현됨
$$E_{\text {layout}}(\mathbf{x}, \mathbf{y})=\sum_{\alpha=1}^{5} w_{\operatorname{la} y, \alpha}^{\top} \phi_{\operatorname{lay}, \alpha}(\mathbf{y})$$
Orientation maps(OM)과 Geometric context(GC)가 사용됨.
OM은 각 pixel의 법선 방향을 추정: VP 배치를 사용하여 이 법선을 wall 으로 변환하는 5차원 feature.
GC는 cutter와 wall에 해당하는 확률을 예측하기 위한 classifier를 사용하는 6차원 feature.